# Duality In Projective Geometry In projective geometry, a mind-blowing concept called Duality exis ts. Before explaining, a real projective space is just an Euclidea n space with additional points at infinity, where parallel lines m eet. So if you are not familiar with projective spaces, you can th ink of them as Euclidean spaces with few exceptions. In a n-dimensional projective space, a r-dimensional object corres ponds to an object of dimension n-1-r. In a projective plane: - A point corresponds to a line, and vice versa. In 3-dimensional: - A point corresponds to a plane, and vice versa. - A Line is self-dual. &c. In a projective space, a statement is equivalent to its dual. In a projective plane: - Two points determine a line, because two lines determine a point In 3-dimensional: - Three points determine a plane, because three planes determine a point. - Two lines determine a plane, because two lines determine a point &c. If they are parallel, they intersect on points at infinity. Many results by duality exist. I will introduce Desargues' theorem , because it is important. ## Desargues' theorem

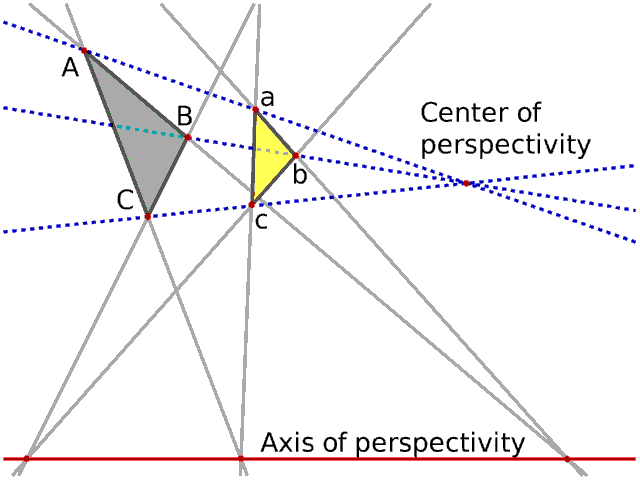
Desargues' theorem is self-dual. It is important, because of its g enerality. For any arithmetically defined projective space over a division ring, it is true. ------------------------------------------------------------------ Theorem. Two triangles are in perspective axially if and only if t hey are in perspective centrally. ------------------------------------------------------------------ Perspective axially means the intersection points (ABab, ACac, BCb c) all lie on a common line. Perspective centrally means the lines determined by the corresponding points of the objects (Aa, Bb, Cc) all meet at a point. It is self-dual. You can interpret the points A, B, C as the lines AB, AC, BC, and vice versa. Proof. By duality, [Two lines determine a point] corresponds to (Two points determine a line). [The lines AB and AC determine the point A] corresponds to (The po ints A and B determine the line AB). [The points A and a determine the line Aa] corresponds to (The lin es AB and ab determine the point ABab). Therefore [The lines Aa, Bb, Cc all intersect at a point] correspo nds to (The points ABab, ACac, BCbc all lie on a line). Q.E.D. To prove, you need only basic geometric structures and duality. Th at's why the theorem is generally true. ## Other dual theorems Ceva's theorem <-> Menelaus' theorem Pascal's theorem <-> Brianchon's theorem are famous. Since Ceva's and Menelaus' theorem are useful for plan e geometry, you might be familiar.