# Duality In Projective Geometry In projective geometry, a mind-blowing concept called Duality exists. Before explaining, a real projective space is just an Euclidean space with additional points at infinity, where parallel lines meet. So if you are not familiar with projective spaces, you can think of them as Euclidean spaces with few exceptions. In a n-dimensional projective space, a r-dimensional object corresponds to an object of dimension n-1-r. In a projective plane: - A point corresponds to a line, and vice versa. In 3-dimensional: - A point corresponds to a plane, and vice versa. - A Line is self-dual. &c. In a projective space, a statement is equivalent to its dual. In a projective plane: - Two points determine a line, because two lines determine a point In 3-dimensional: - Three points determine a plane, because three planes determine a point. - Two lines determine a plane, because two lines determine a point &c. If they are parallel, they intersect on points at infinity. Many results by duality exist. I will introduce Desargues' theorem, because it is important. ## Desargues' theorem

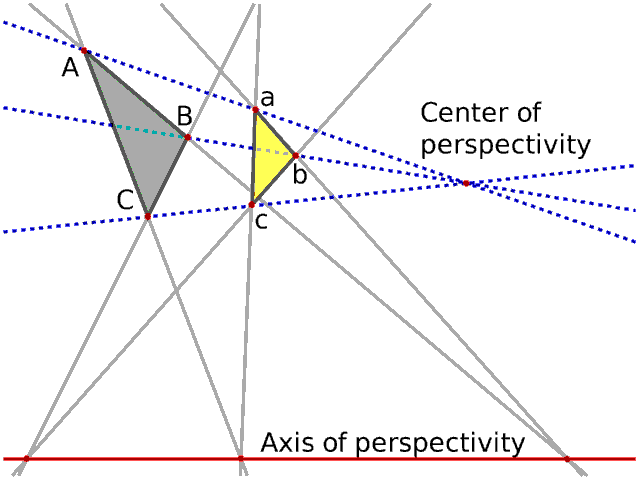
Desargues' theorem is self-dual. It is important, because of its generality. For any arithmetically defined projective space over a division ring, it is true. ------------------------------------------------------------------ Theorem. Two triangles are in perspective axially if and only if they are in perspective centrally. ------------------------------------------------------------------ Perspective axially means the intersection points (ABab, ACac, BCbc) all lie on a common line. Perspective centrally means the lines determined by the corresponding points of the objects (Aa, Bb, Cc) all meet at a point. It is self-dual. You can interpret the points A, B, C as the lines AB, AC, BC, and vice versa. Proof. By duality, [Two lines determine a point] corresponds to (Two points determine a line). [The lines AB and AC determine the point A] corresponds to (The points A and B determine the line AB). [The points A and a determine the line Aa] corresponds to (The lines AB and ab determine the point ABab). Therefore [The lines Aa, Bb, Cc all intersect at a point] corresponds to (The points ABab, ACac, BCbc all lie on a line). Q.E.D. To prove, you need only basic geometric structures and duality. That's why the theorem is generally true. ## Other dual theorems Ceva's theorem <-> Menelaus' theorem Pascal's theorem <-> Brianchon's theorem are famous. Since Ceva's and Menelaus' theorem are useful for plane geometry, you might be familiar.